Sistemas Lineares 3 x 3
Considere o Sistemas:
\(\begin{cases}a_1x+b_1y+c_1z=d_1 \\ a_2x+b_2y+c_2z=d_2 \\ a_3x+b_3y+c_3z=d_3 \end{cases}\)
de três equações e três incógnita. Geometricamente, cada uma das equações, nessa ordem, define os planos π1,π2 e π3, respectivamente. O termo (x,y,z) é a solução desse sistema quando o P(x,y,z) pertencerem à intersecção π1 ∩ π2 ∩ π3 , ou seja, quando P está simultaneamente nos três planos.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}-3x-9y+z=4 \\ 5x+y+2z=2 \\ -x+2y+9z=10 \end{cases}\)
temos os planos: π1 = - 3x - 9y + z = 4, π2 = 5x + y + 2z = 2 e π3 = -x + 2y + 9z = 10 onde a P = (-0.01,-0.31,1.18) é a solução do sistema.
Observe a figura:
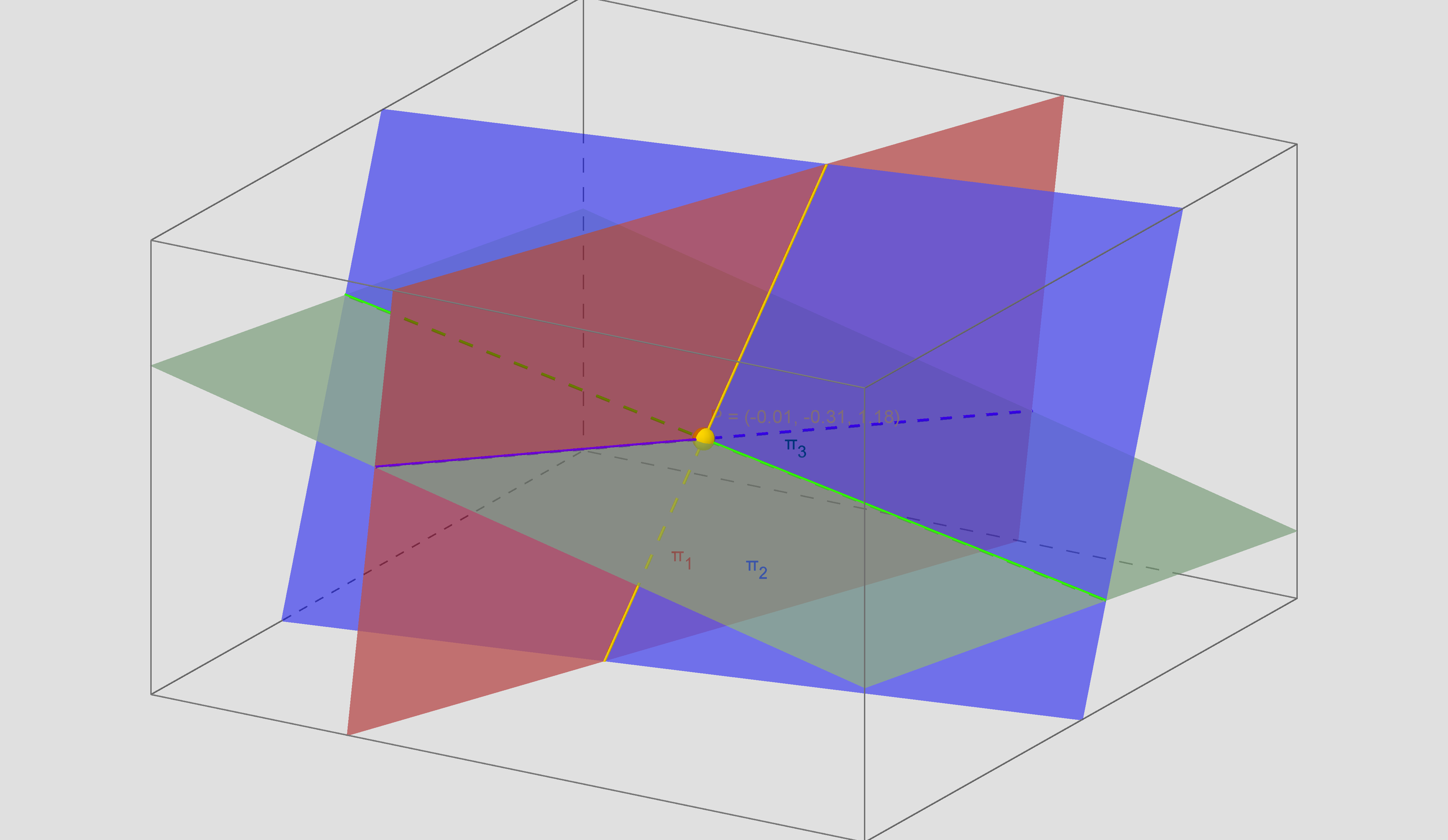
O ponto P amarelo é a solução do sistema
π1 é o plano vermelho, π2 é o plano azul e π3 é o plano vermelho
Possibilidades para as posições relativas dos três planos no espaço
Existem oito possibilidades para as posições relativas dos três planos, π1,π2 e π3, no espaço.
1ª Possibilidade: os três planos coincidem
Neste caso, todos os pontos P(x,y,z) de π1 são soluções do sistema. Há portanto, infinitas soluções para o sistema.
O sistema é possível e indeterminado (SPI).
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+2y-z=3 \\ 2x+4y-2z=6 \\ 3x+6y-3z=9 \end{cases}\)
temos L1 = (1,2,-1,3), L2 = (2,4,-2,6),L3 = (3,6,-3,9), logo L2 = 2L1 e L3 = 3L1.
Observe a figura:
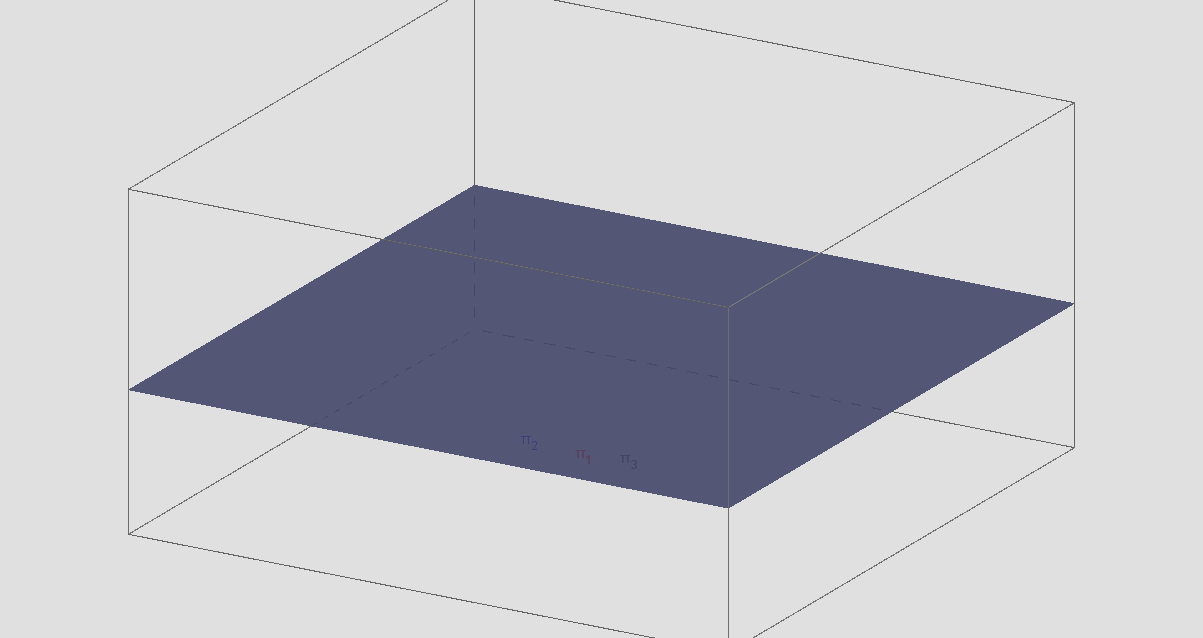
sistema é possível e indeterminado
π1 = π2 = π3
2ª dois planos coincidem e o terceiro é paralelo a eles
Neste caso, o sistema é impossível, não possui solução (SI).
Pode-se provar que isso ocorre quando L2 é múltipo de L1, ou seja, L2 = kL1 o que accarreta l2 = kl1; l3 = ml1; mas L3 não é múltiplo de L1.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y-z=1 \\ 2x+2y-2z=2 \\ 4x+4y-4z=7 \end{cases}\)
temos L2 = (1,1,-1,1), L2 = (2,2,-2,2),L3 = (4,4,-4,7), logo l2 = 2l1; l3 = 4l1; mas L3 não é múltiplo de L1. Lógo, o sistema não tem solução; é impossível.
Observe a figura:
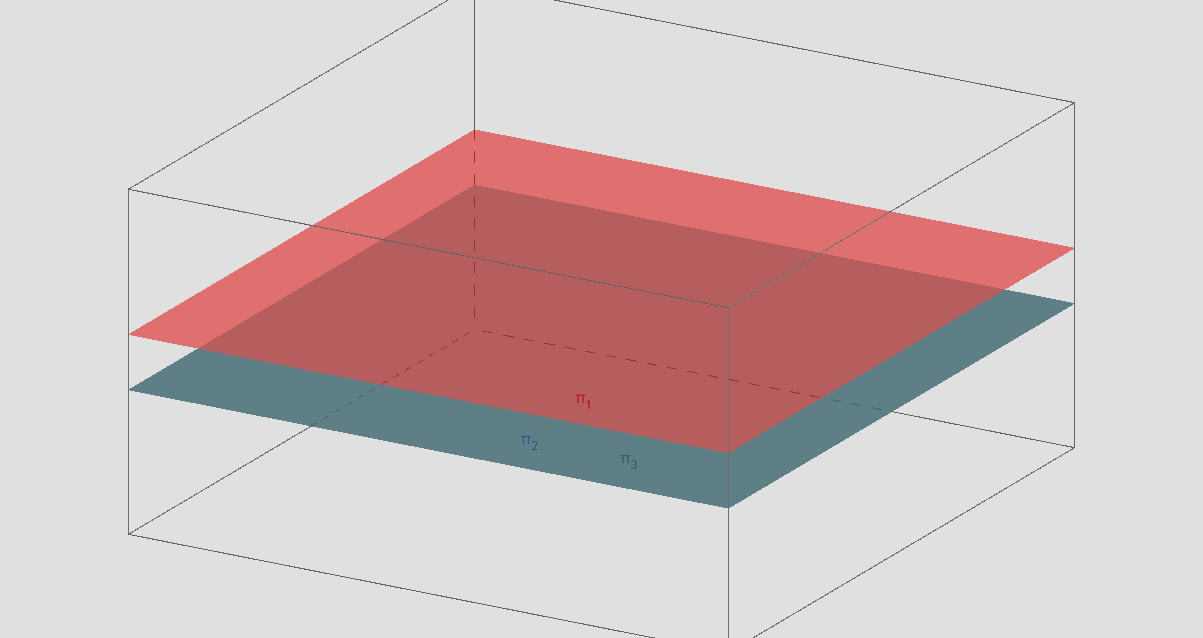
sistema é impossivel
π2 = π3 e π1 || π2
3ª dois planos coincidem e o terceiro os intersecta segundo uma reta
Nesse caso, todos os pontos P(x,y,z) da reta são solução. Há, portanto, infinitas soluções. O sistema é pssivel e indeterminado (SPI). Pode-se provar que isso ocorre quando L2 = kL1 (e, portanto, l2 = kl1); mas l3 não é múltiplo de l1.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y-z=1 \\ 2x+2y-2z=2 \\ 4x+4y-z=4 \end{cases}\)
temos π1 = π2, mas l3 = (4,4,-1) não é múltiplo de l1 = (1,1,-1). Assim, π1 ∩ π3 é a reta r que é a solução do sistema.
Observe a figura:
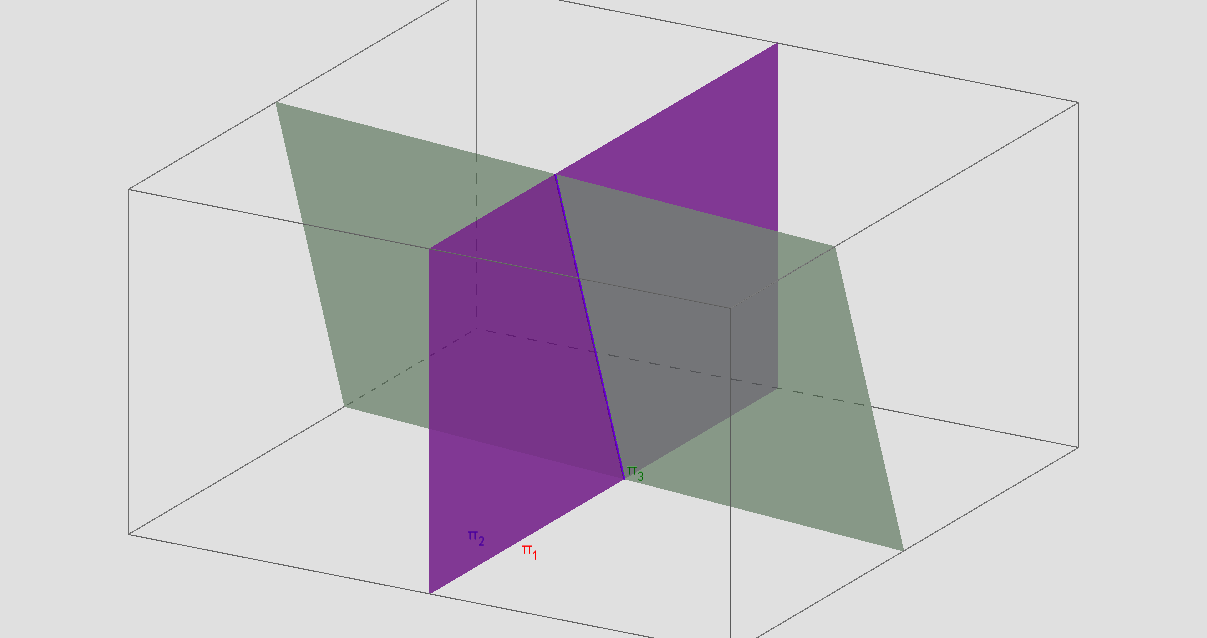
sistema é possível e indeterminado
π1 = π2 e π1 ∩ π3
4ª os planos são paralelos dois a dois
Nesse caso, o sistema não possui solução; é imossivel (SI). Pode-se provar que isso ocorre quando cada um dos vetores, l1, l2 e l3 é multiplo do outro, mas os vetores L1, L2 e L3 não são múltiplo um do outro, dois a dois.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y-z=1 \\ 2x+2y-2z=3 \\ 4x+4y-4z=7 \end{cases}\)
temos L1 = (1,1,-1,1) e l1 = (1,1,-1); L2 = (2,2,-2,3) e l2 = (2,2,-2); L3 = (4,4,-4,7) e l3 = (4,4,-4) como l1, l2 e l3 são múltiplo um do outro, mas L1, L2 e L3 não são múltiplo um do outro.
Observe a figura:

sistema é impossível
π1 || π2 || π3
5ª dois planos paralelos e o outro os intersectasegundo retas paralelas r e s
π1 e π2 são paralelos. Logo, π1 ∩ π2 = ∅. Isso acarreta que π1 ∩ π2 ∩ π3 = ∅. Portanto, o sistema não possui solução; é impossível (SI).
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y-z=1 \\ 2x+2y-2z=3 \\ 4x+4y-z=4 \end{cases}\)
Observe que l2 = (2,2,-2), l1 = (1,1,-1) e l2 = 2l1, porém L2 = (2,2,-2,3), L1 = (1,1,-1,1) não é múltiplo. Como também l3 = (4,4,-1) não é múltiplo de l1 = (1,1,-1). Logo o sistema é impossível.
Observe a figura:
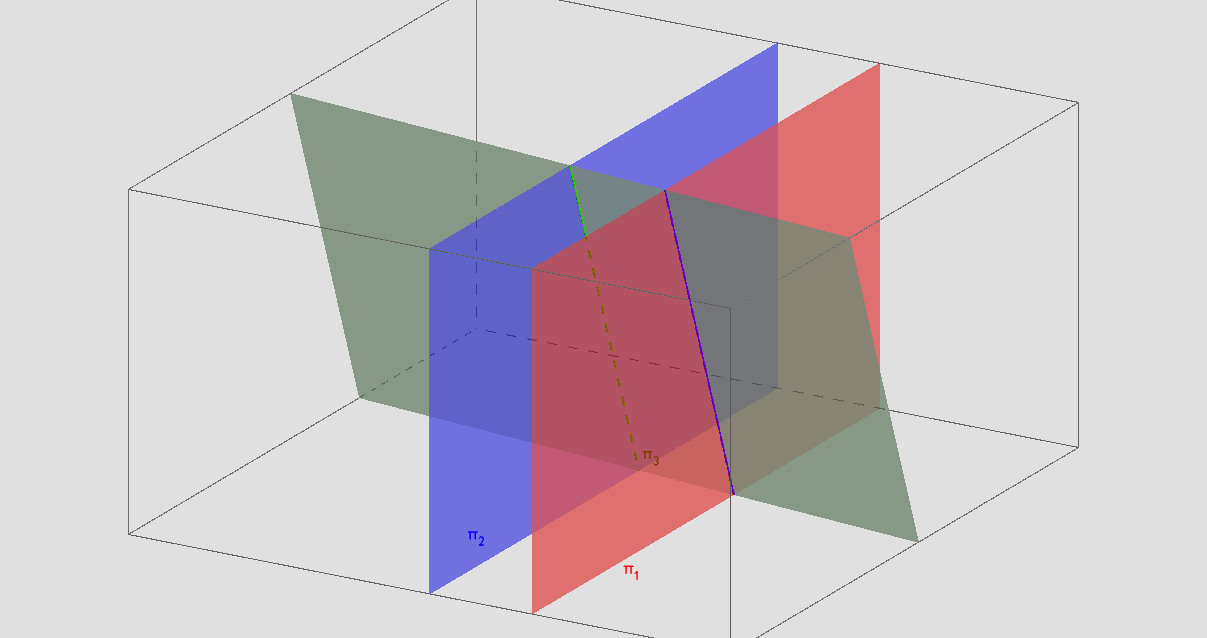
sistema é impossível
π1 ∩ π2 ∩ π3 = ∅
6ª os três planos são distintos em têm uma reta em comum
Neste caso todos os pontos P(x,y,z) da reta r são soluções. Há, portanto, infinitas soluções.
O sistema é possível e indeterminado (SPI). Pode-se provar que isso ocorre quando nenhum dos vetores l1, l2 e l3 é múltiplo do outro e L3 pode ser combinação linear de L1 e L2, isso é L3 = kL2 + mL1.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y+z=1 \\ 2x-y+z=5 \\ 4x+y+3z=7 \end{cases}\)
Temos L1=(1,1,1,1) e l1=(1,1,1); L2=(2,-1,1,5) e l2=(2,-1,1); L3=(4,1,3,7) e l1=(4,1,3).
observe que nenhum dos vetores l1, l2 e l3 é multiplo do outro. E, também, que L3 = 2L1 + L2, logo o sistema é possível e indeterminado
Observe a figura:
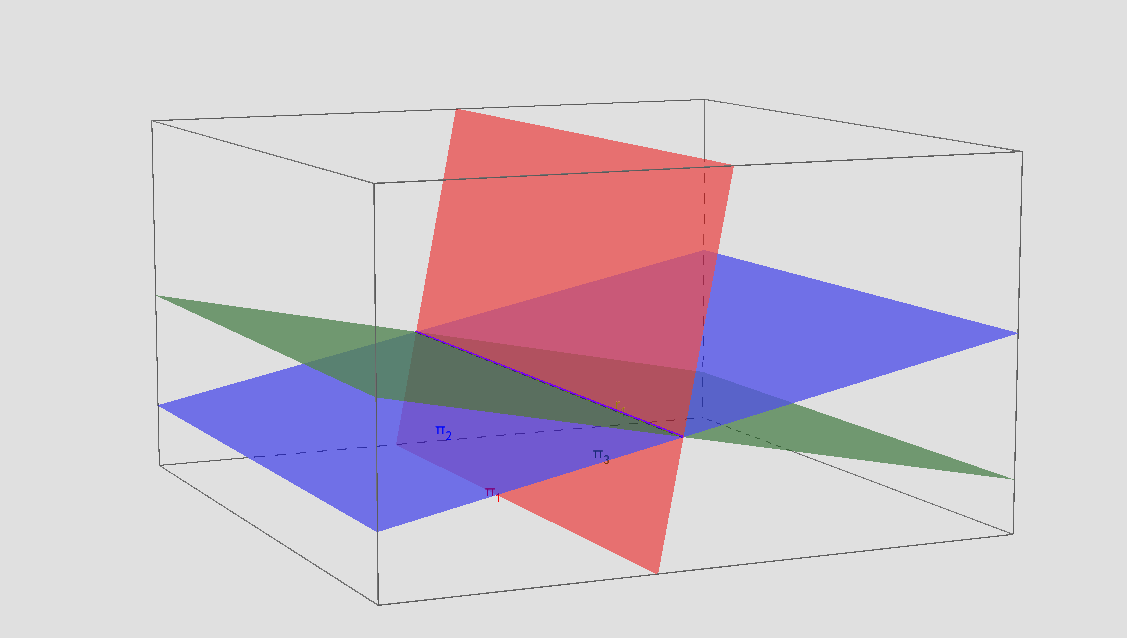
sistema é possível e indeterminado
π1 ∩ π2 ∩ π3 = r
7ª os três planos se intersectam, dois a dois, segundo retas paralelas umas às outras
Nesse caso, o sistema é impossível (SI)
Os vetores l1, l2 e l3 não são multiplos um dos outro, pois não há paralelismo nem coincidência entre nenhum dos planos. Além disso, é possível provar que l3 = kl1 + ml2 e L3 ≠ kL1 + mL2
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y-3z=1 \\ 5x+2y+z=2 \\ 9x+3y+5z=5 \end{cases}\)
Temos L1=(1,1,-3,1) e l1=(1,1,-3); L2=(5,2,1,2) e l2=(5,2,1); L3=(9,3,5,5) e l1=(9,3,5).
observe que nenhum dos vetores l1, l2 e l3 não são multiplo do outro. E, l3 = 2l2 - l1, mas L3 ≠ 2L2 - L1.
Portando, este sistema é impossível
Observe a figura:
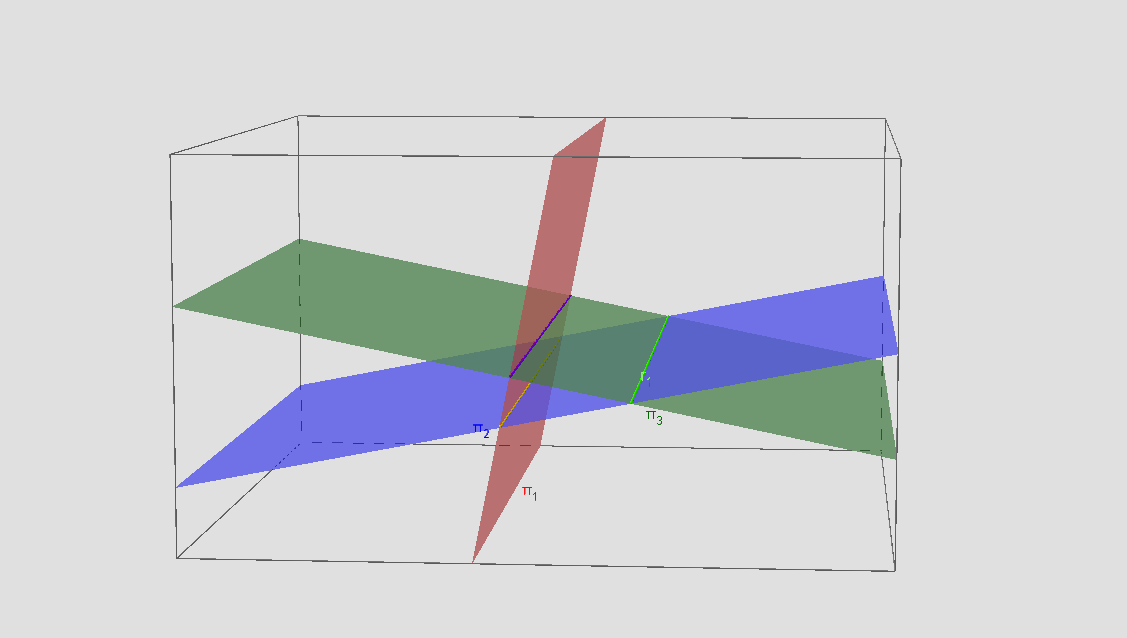
sistema é impossível
π1 ∩ π2 = r, π3 ∩ π3 = s e r ∩ s = ∅
8ª os três planos têm um único ponto em comum
Nesse caso o sistema é possível e determinado (SPD)
É possível provar que o sistema tem uma única solução se, e somente se, os vetores l1, l2 e l3 são linearmentes independentes.
Exemplo:
Seja o Sistema Linear:
\(\begin{cases}x+y+z=1 \\ 2x-y+z=5 \\ 4x+y+3z=7 \end{cases}\)
temos l1 = (1,2,-3), l2 = (2,3,4) e l3 = (4,7,-1)
Como o determinante de \(\left( \begin{array}{cc} 1 & 2 & -3 \\ 2 & 3 & 4 \\ 1 & 2 & -3 \end{array} \right)\) = -1 ≠ 0, os vetores são LI. Portanto o sistema é possível e determinado.
Observe a figura:
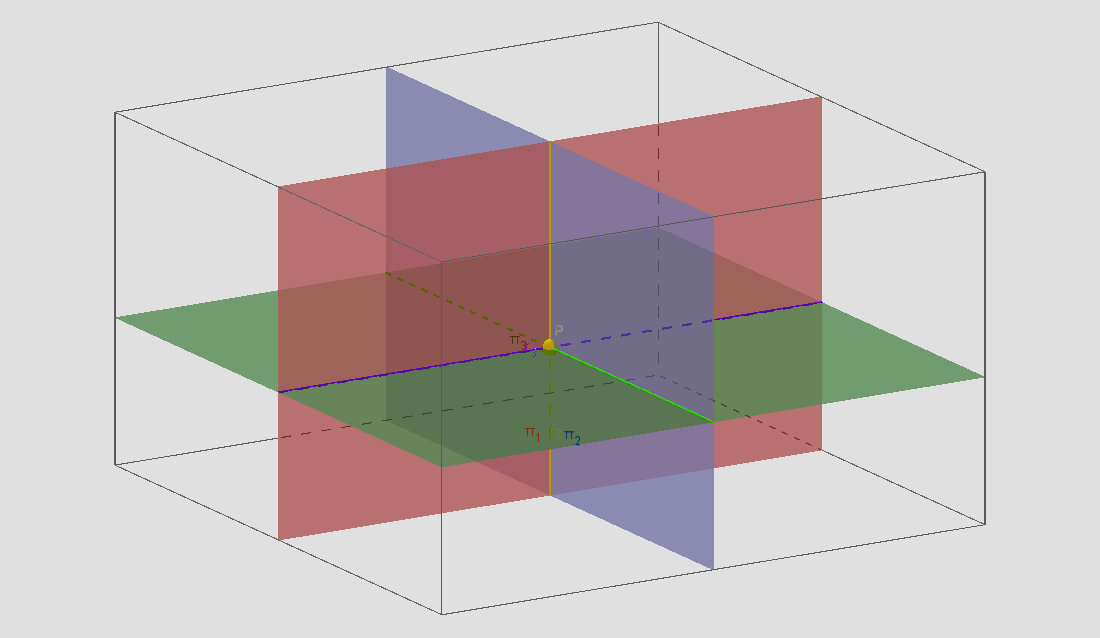
sistema é possível
π1 ∩ π2 ∩ π3 = P

