Sistemas Lineares 2 x 2
Considere o Sistemas:
\(\begin{cases}y = a_1x + b_1 \\ y= a_2x+b_2 \end{cases}\)
de duas equações e duas incógnita. Geometricamente, cada uma das equações, nessa ordem, definem as retas r1 e r2 respectivamente.
Quando r1 ∩ r2 = P, o sistema é possivel e determinado.
Quando r1 ∩ r2 = ∅, o sistema é impossível.
Quando r1 ∩ r2 = r, o sistema é possivel e indetermindado.
EXEMPLO 1
Dado o sistema:
\(\begin{cases}y =-x+2 \\ y=x+8 \end{cases}\)
temos que as equações possuem coeficientes angulares diferentes, sendo assim o sistema é possivel e determinado.
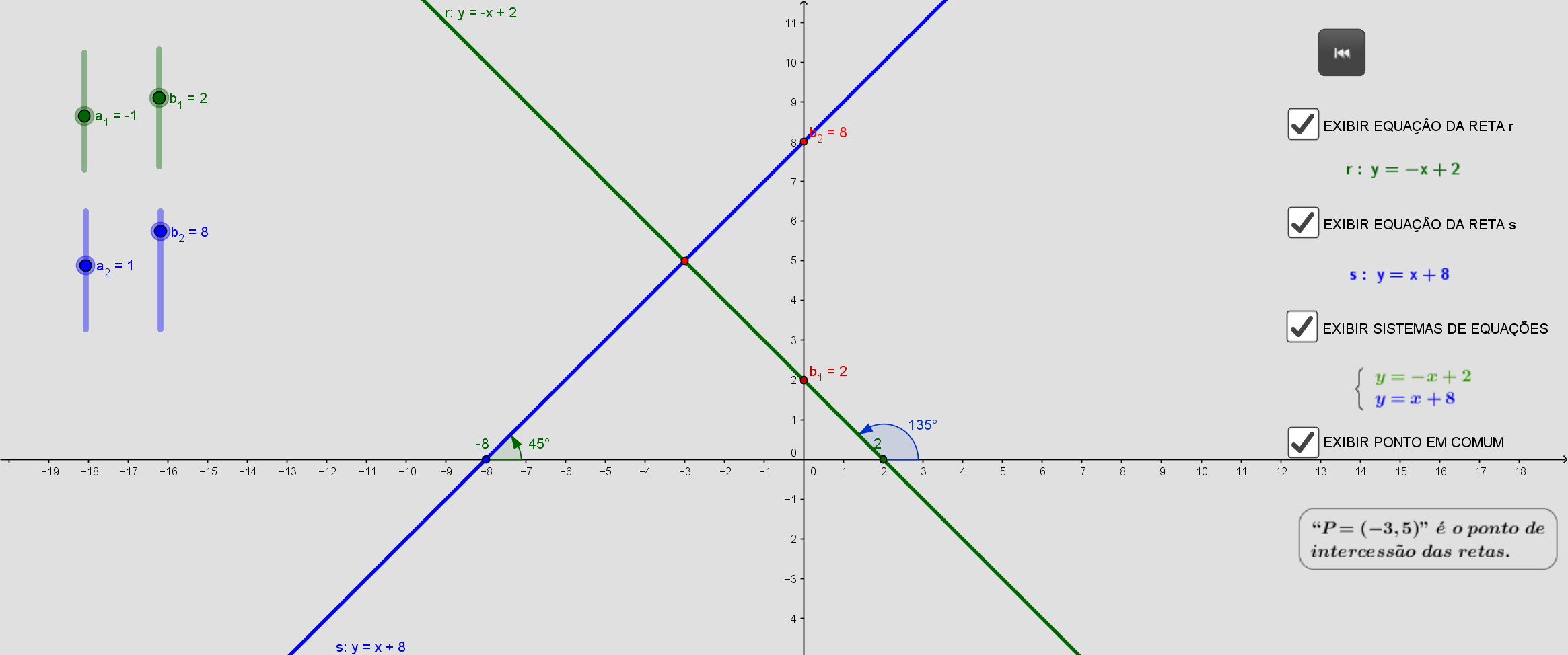
sistema é possível e determinado
r1 ∩ r2 = P(-3,5)
EXEMPLO 2
Dado o sistema:
\(\begin{cases}y =x+4 \\ y=x+6 \end{cases}\)
temos que as equações possuem coeficientes angulares iguais e suas variaveis independentes diferentes, sendo assim o sistema é impossível.
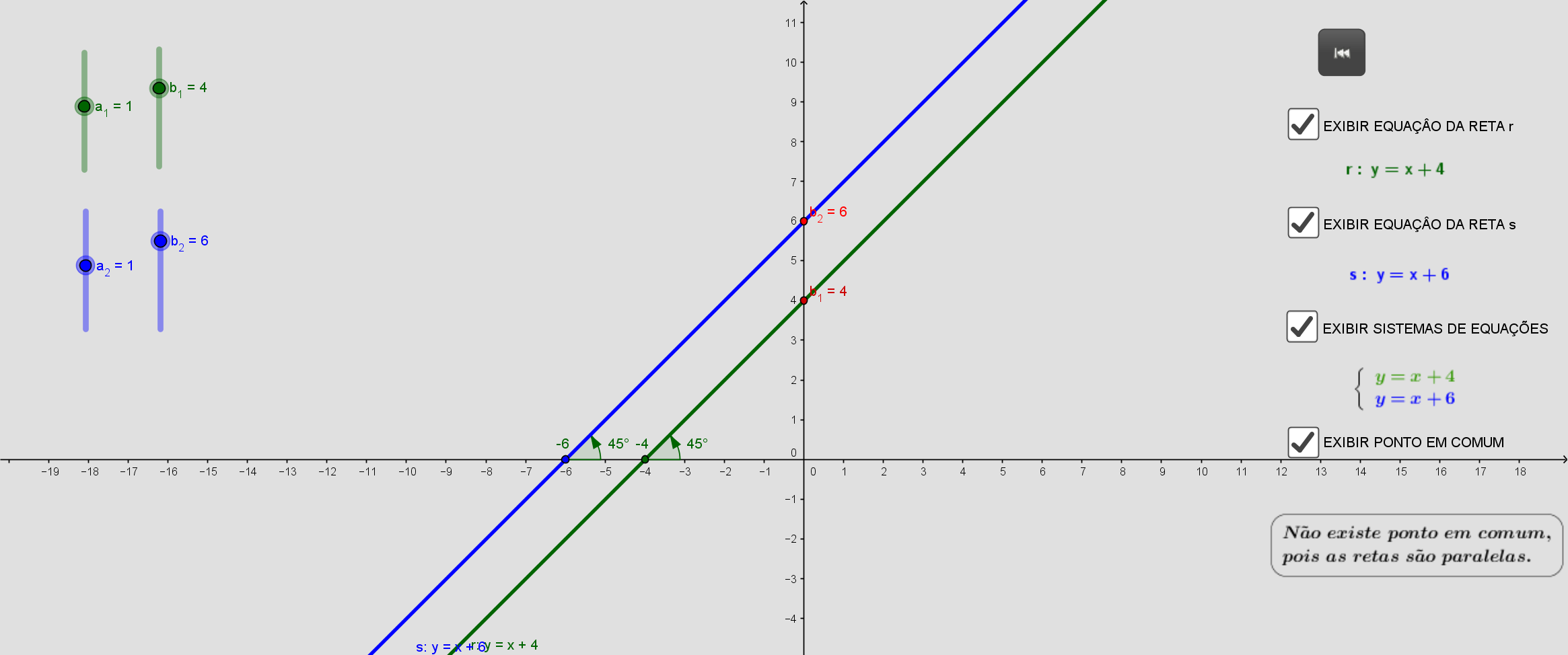
sistema é impossível
r1 ∩ r2 = ∅
EXEMPLO 3
Dado o sistema:
\(\begin{cases}y =x+4 \\ y=x+4 \end{cases}\)
temos que as equações possuem coeficientes angulares e a variavel independentes são iguais, sendo assim o sistema é possível e indeterminado.
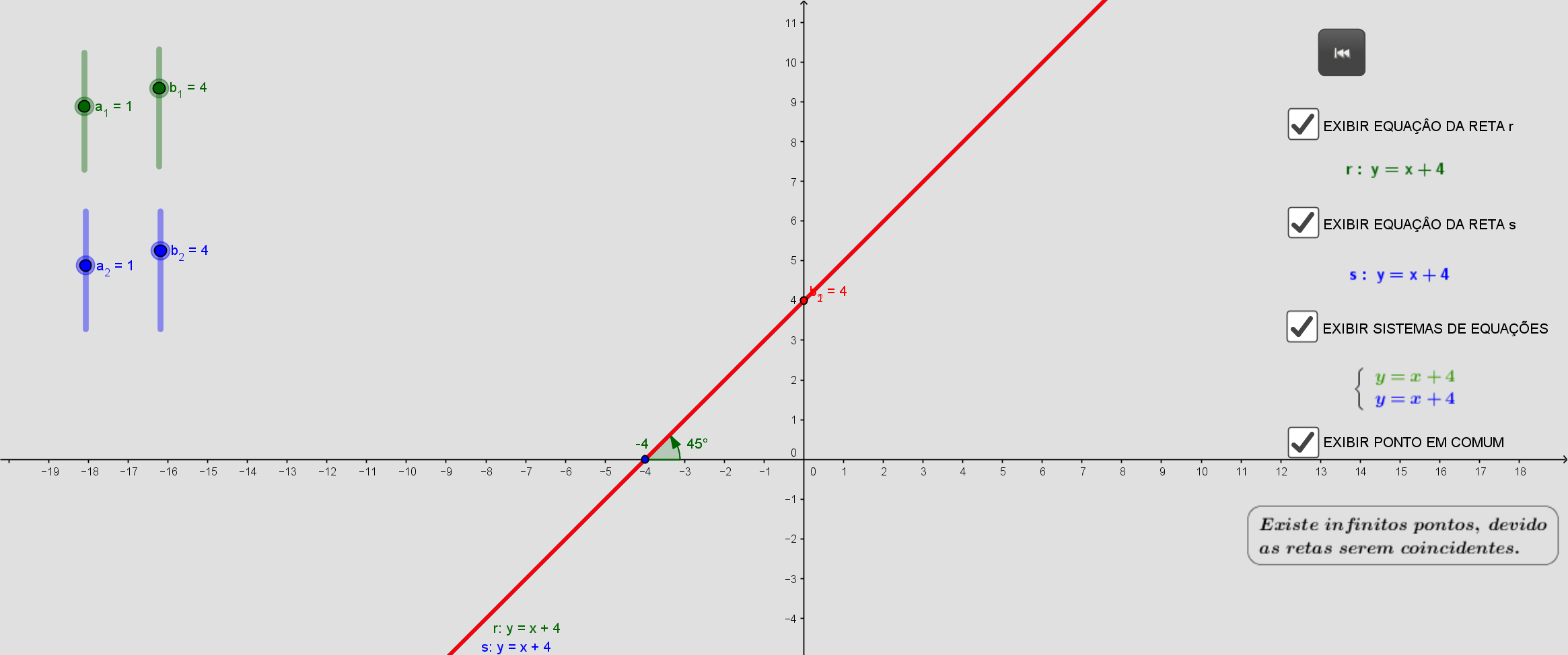
sistema é possível e indeterminado
r1 ∩ r2 = r
Considere agora o Sistemas:
\(\begin{cases}a_1x + b_1y = c_1 \\ a_2x+b_2y = c_2 \end{cases}\)
de duas equações e duas incógnita. Geometricamente, cada uma das equações, nessa ordem, definem as retas r1 e r2 respectivamente.
Quando r1 ∩ r2 = P, o sistema é possivel e determinado.
Quando r1 ∩ r2 = ∅, o sistema é impossível.
Quando r1 ∩ r2 = r, o sistema é possivel e indetermindado.
EXEMPLO 4
Dado o sistema:
\(\begin{cases}-9x+9y=0 \\ -2x+2y=-4 \end{cases}\)
temos que as equações possuem coeficientes angulares diferentes e \(\frac{a_1}{a_2}\)≠ \(\frac{b_1}{b_2}\) ⇒ o sistema é possível e determinado.
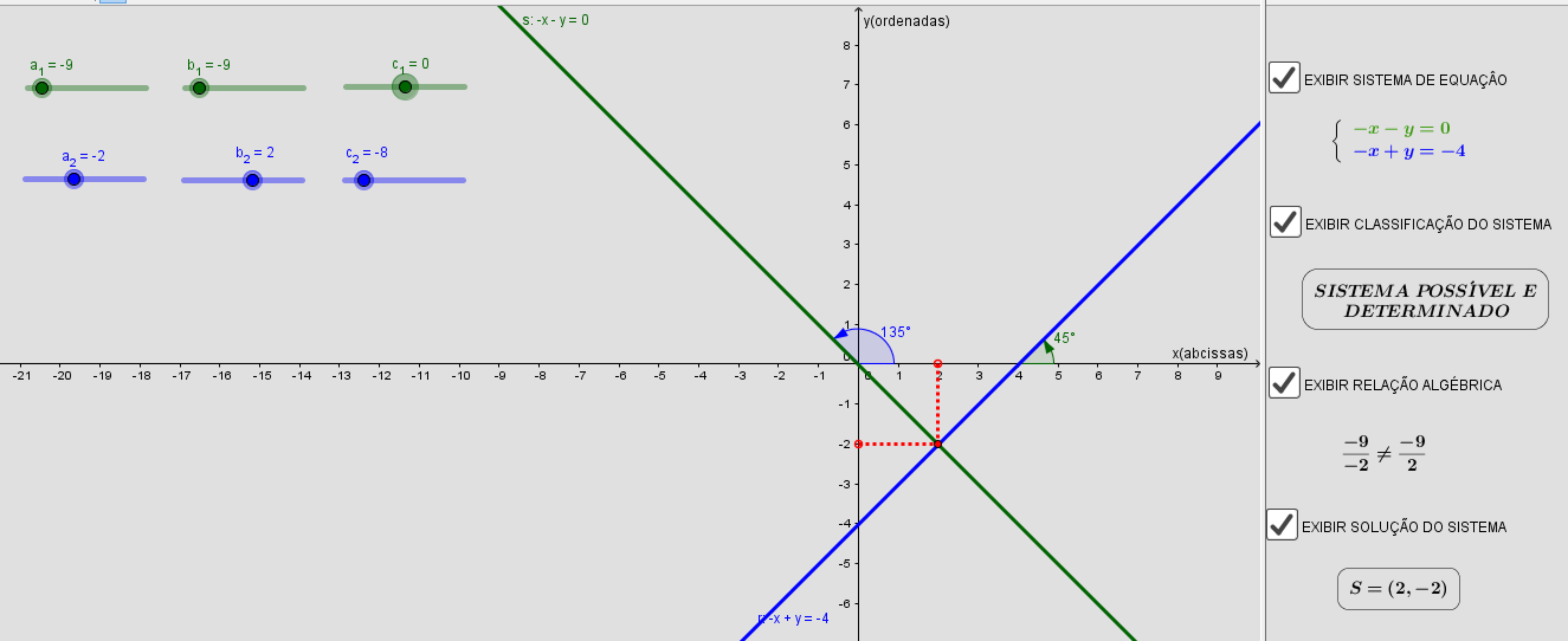
sistema é possível e determinado
r1 ∩ r2 = P(2,-2)
EXEMPLO 5
Dado o sistema:
\(\begin{cases}-9x+9y=0 \\ -2x+2y=-4 \end{cases}\)
temos que as equações possuem coeficientes angulares iguais e \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\) ⇒ o sistema é impossível.
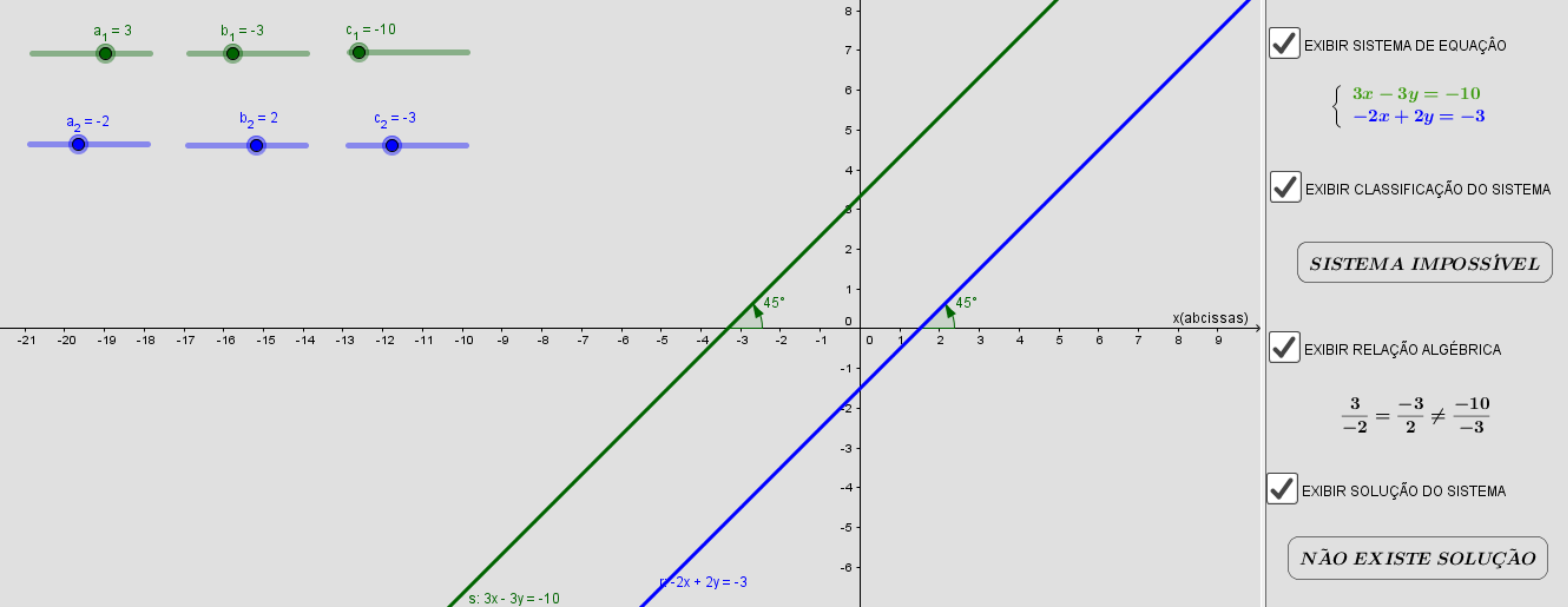
sistema é possível e determinado
r1 ∩ r2 = ∅
EXEMPLO 6
Dado o sistema:
\(\begin{cases}-9x-9y=9 \\ -2x-2y=2\end{cases}\)
temos que as equações possuem coeficientes angulares iguais e \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) ⇒ o sistema é possível e indeterminado.
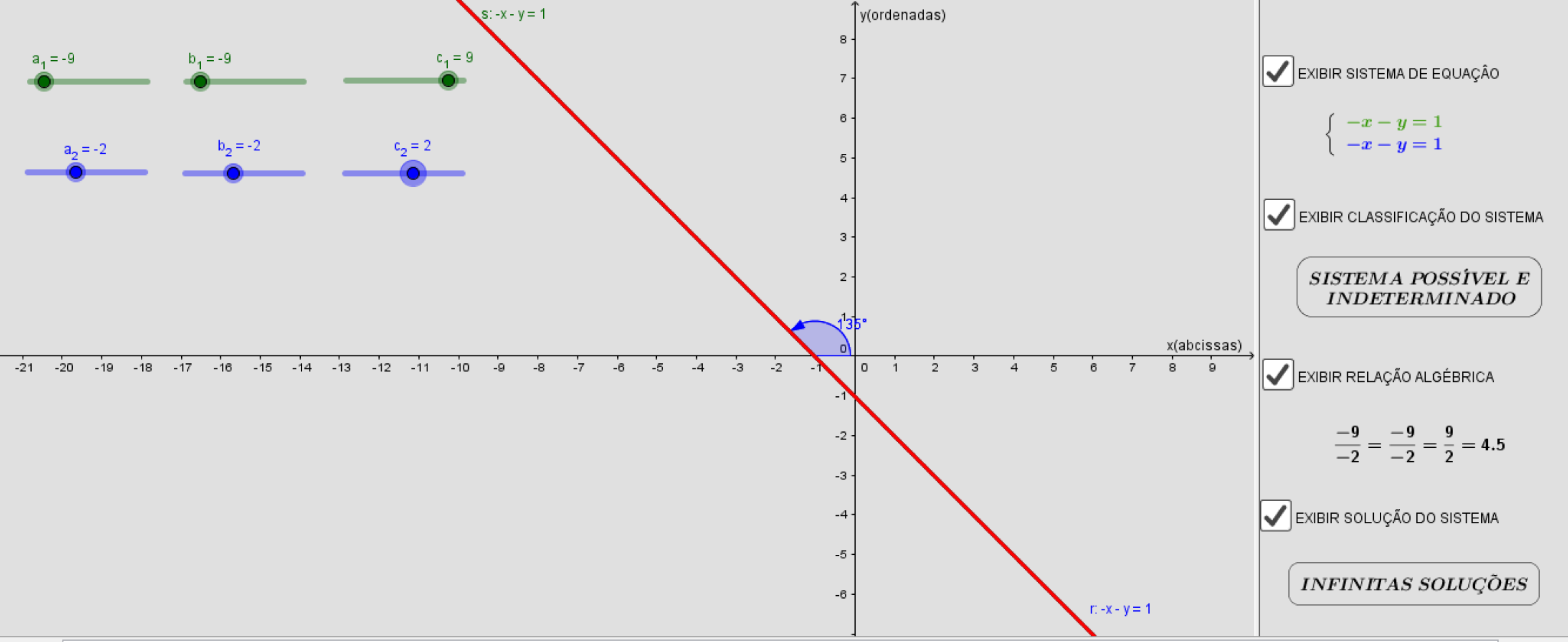
sistema é possível e indeterminado
r1 ∩ r2 = r
Observe que as equações r1 e r2 são equivalentes a equação -x - y = 1.
Sistemas Lineares 2 x 2 homogêneos
Se em um sistema linear todos os termos independentes são nulos, o sistema é denomindado sistema linear homogênio.
Assim o sistema linear homogêneo:
\(\begin{cases}a_1x+b_1y=0 \\ a_2x+b_2y=0\end{cases}\)
Nota-se que o sistema linear homogênio adimite sempre solução, pos o sistema sempre adimite solução (0,0) denominada solução trivial ou imprópria
EXEMPLO 1
Dado o sistema:
\(\begin{cases}2x-2y=0 \\ 2x-1y=0\end{cases}\)
temos que as P=(0,0) é o sistema é possivel e determinado
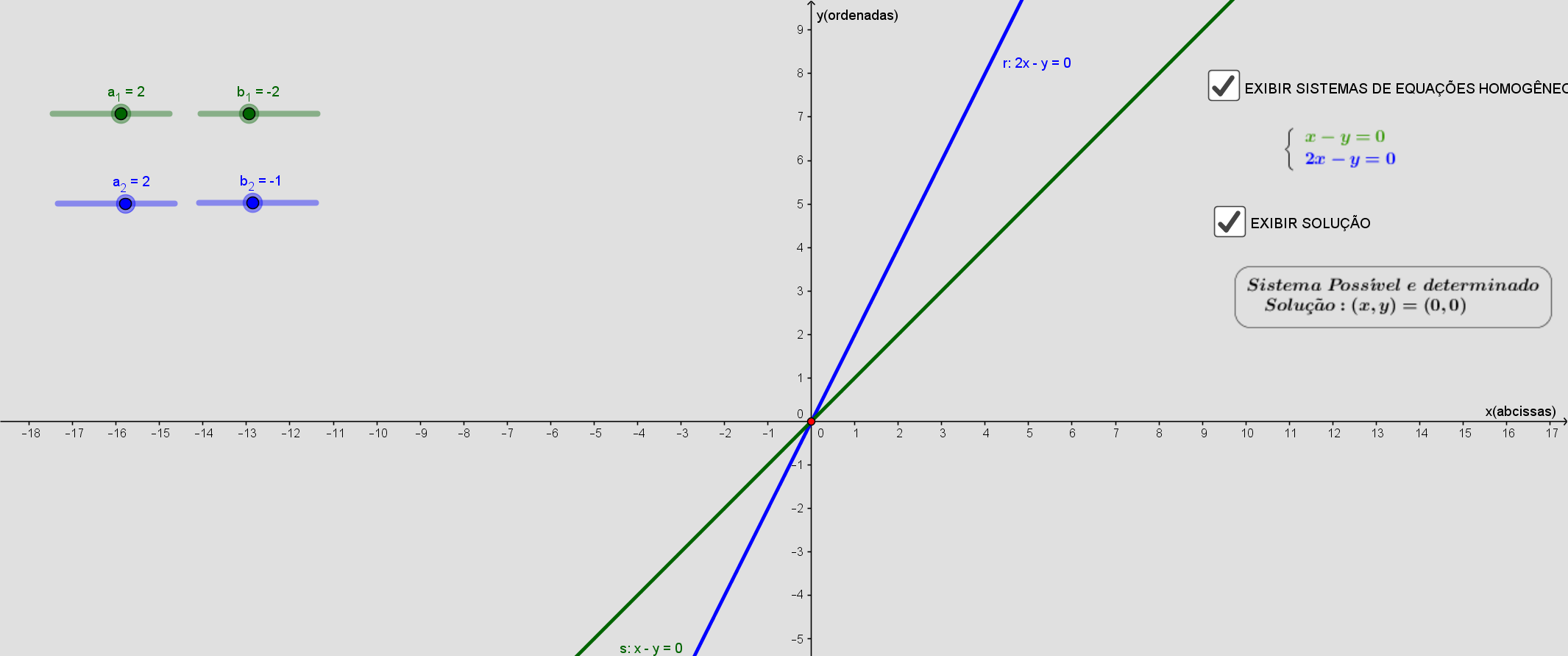
sistema é possível e determinado
r1 ∩ r2 = P(0,0)
EXEMPLO 2
Dado o sistema:
\(\begin{cases}2x-2y=0 \\ 2x-2y=0\end{cases}\)
temos que as r1 = r2, logo é o sistema é possivel e indeterminado
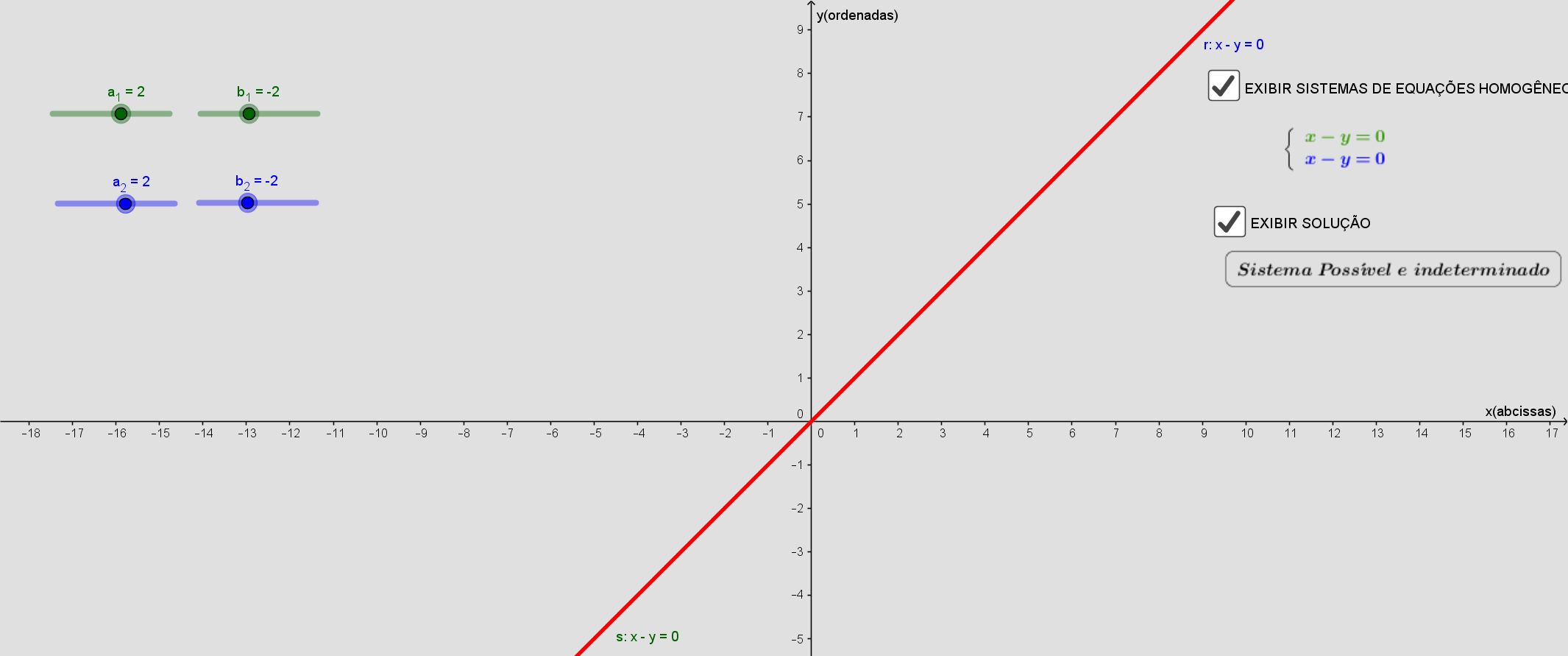
sistema é possível e indeterminado
r1 ∩ r2 = r

